<div id="article-body">
<p>Regarde attentivement! Les mathématiciens ont inventé une nouvelle forme à 13 côtés qui peut être carrelée à l&rsquo;infini sans jamais répéter un motif. Ils l&rsquo;appellent « l&rsquo;einstein ».</p>
<p>Pendant des décennies, les mathématiciens se sont demandé s&rsquo;il était possible de trouver une seule forme spéciale qui pourrait parfaitement carreler une surface, sans laisser de vides ni provoquer de chevauchements, le motif ne se répétant jamais. Bien sûr, cela n&rsquo;a rien à voir avec un motif qui se répète &#8211; il suffit de regarder le sol d&rsquo;une salle de bain ou d&rsquo;une cuisine, qui est probablement composé de simples carreaux rectangulaires. Si vous deviez prendre votre sol et le déplacer (appelé une « translation » en mathématiques), vous pourriez trouver une position où le sol a exactement la même apparence qu&rsquo;avant, prouvant qu&rsquo;il s&rsquo;agit d&rsquo;un motif répétitif.</p>
<aside class="hawk-nest" data-render-type="fte" data-skip="dealsy" data-widget-type="seasonal"></aside>
<p>En 1961, le mathématicien Hao Wang a supposé que les pavages apériodiques, ou les pavages qui ne deviennent jamais un motif répétitif, étaient impossibles. Mais son propre étudiant, Robert Berger, l&rsquo;a déjoué, trouvant un ensemble de 20 426 formes qui, lorsqu&rsquo;elles sont soigneusement arrangées, ne se répètent jamais. Il a ensuite réduit cela à un ensemble de 104 tuiles. Cela signifie que si vous deviez acheter un ensemble de ces carreaux, vous pourriez les disposer sur le sol de votre cuisine et ne jamais trouver de motif répétitif.</p>
<p>Dans les années 1970, le physicien lauréat du prix Nobel Roger Penrose a trouvé un ensemble de seulement deux tuiles qui pouvaient être arrangées ensemble dans un motif non répétitif, maintenant connu sous le nom de pavage de Penrose.</p>
<p><img class="expandable lazy-image-van" src="https://thebuzzly.com/wp-content/uploads/2023/04/La-tuile-einstein-recemment-decouverte-est-une-forme.jpg" alt="Ici, nous voyons les quatre premières itérations du métatile H et de ses supertiles." data-normal="https://vanilla.futurecdn.net/livescience/media/img/missing-image.svg" data-srcset="https://cdn.mos.cms.futurecdn.net/FyLiKsuxpLzJ6Sik6TuMyB-320-80.jpg 320w, https://cdn.mos.cms.futurecdn.net/FyLiKsuxpLzJ6Sik6TuMyB-480-80.jpg 480w, https://cdn.mos.cms.futurecdn.net/FyLiKsuxpLzJ6Sik6TuMyB-650-80.jpg 650w, https://cdn.mos.cms.futurecdn.net/FyLiKsuxpLzJ6Sik6TuMyB-970-80.jpg 970w, https://cdn.mos.cms.futurecdn.net/FyLiKsuxpLzJ6Sik6TuMyB-1024-80.jpg 1024w, https://cdn.mos.cms.futurecdn.net/FyLiKsuxpLzJ6Sik6TuMyB-1200-80.jpg 1200w" data-sizes="(min-width: 1000px) 970px, calc(100vw - 40px)" data-pin-media="https://thebuzzly.com/wp-content/uploads/2023/04/La-tuile-einstein-recemment-decouverte-est-une-forme.jpg" /></p>
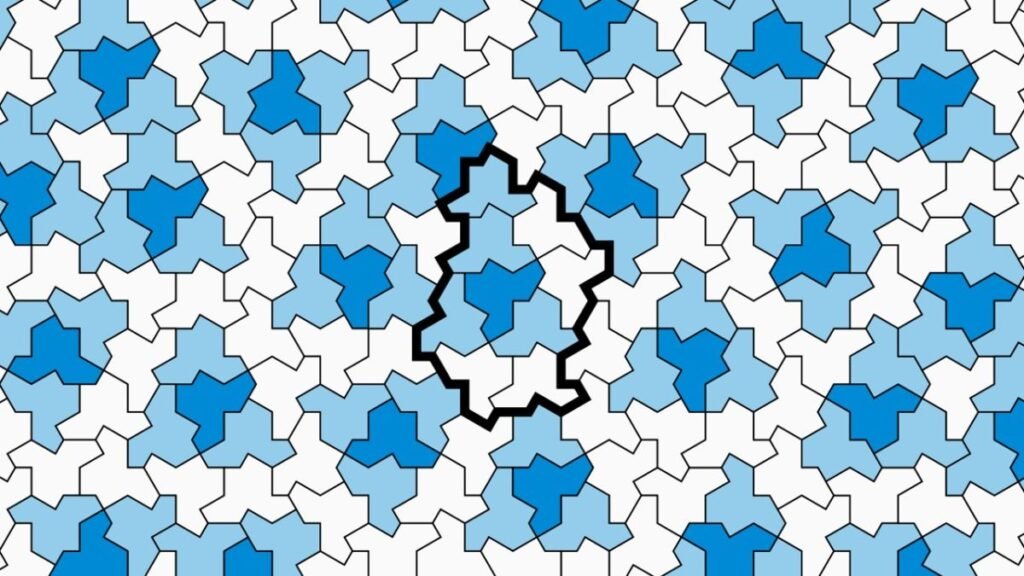
<figure class="van-image-figure inline-layout" data-bordeaux-image-check=""><figcaption class=" inline-layout"><span class="caption-text">Ici, nous voyons les quatre premières itérations du métatile H et de ses supertiles. </span><span class="credit">(Crédit image : Smith el at. (2023))</span></figcaption></figure>
<p>Depuis lors, les mathématiciens du monde entier ont recherché le saint graal du pavage apériodique, appelé « l&rsquo;einstein ». Le mot ne vient pas de <u>le célèbre Albert</u> mais de la traduction allemande de son nom de famille : une pierre. Une seule tuile &#8211; une « pierre » &#8211; pourrait-elle remplir un espace bidimensionnel sans jamais répéter le motif qu&rsquo;elle crée ?</p>
<p>La réponse vient d&rsquo;être découverte par David Smith, un technicien d&rsquo;impression à la retraite de l&rsquo;East Yorkshire, en Angleterre. Comment a-t-il trouvé cette solution remarquable ? « Je suis toujours en train de déconner et d&rsquo;expérimenter avec des formes », a déclaré Smith <a href="https://www.nytimes.com/2023/03/28/science/mathematics-tiling-einstein.html" target="_blank" rel="nofollow noopener" data-url="https://www.nytimes.com/2023/03/28/science/mathematics-tiling-einstein.html"><u>Le New York Times</u></a><span class="sr-only"> (s&rsquo;ouvre dans un nouvel onglet)</span>. « C&rsquo;est toujours agréable de mettre la main à la pâte. Cela peut être assez méditatif. »</p>
<p>Smith et ses co-auteurs ont surnommé la nouvelle forme « le chapeau », principalement parce qu&rsquo;il ressemble vaguement à un feutre. Bien que les mathématiciens aient connu la forme, qui a 13 côtés, ils ne l&rsquo;avaient jamais considérée comme un candidat pour le pavage apériodique.</p>
<p>« Dans un certain sens, il est resté assis là tout ce temps, attendant que quelqu&rsquo;un le trouve », <a href="https://www.smith.edu/academics/faculty/marjorie-senechal" target="_blank" rel="nofollow noopener" data-url="https://www.smith.edu/academics/faculty/marjorie-senechal"><u>Marjorie Sénéchal</u></a><span class="sr-only"> (s&rsquo;ouvre dans un nouvel onglet)</span>un mathématicien du Smith College qui ne faisait pas partie de l&rsquo;étude, a déclaré au Times.</p>
<p>Smith a travaillé en étroite collaboration avec deux informaticiens et un autre mathématicien pour développer deux preuves montrant que « le chapeau » est un monotile apériodique &#8211; un einstein. Une preuve liée à la construction d&rsquo;ensembles hiérarchiques de tuiles de plus en plus grands, montrant comment le motif ne se répète jamais à mesure que la surface augmente. L&rsquo;autre preuve concernait la découverte par l&rsquo;équipe qu&rsquo;il n&rsquo;y avait pas qu&rsquo;une seule de ces tuiles, mais un ensemble infini de formes apparentées qui pouvaient toutes faire l&rsquo;affaire. Le document de l&rsquo;équipe est disponible sur le <a href="https://arxiv.org/abs/2303.10798" target="_blank" rel="nofollow noopener" data-url="https://arxiv.org/abs/2303.10798"><u>serveur de préimpression arXiv</u></a><span class="sr-only"> (s&rsquo;ouvre dans un nouvel onglet)</span> mais n&rsquo;a pas encore été examiné par des pairs et les preuves n&rsquo;ont pas encore été examinées.</p>
<p>Ces types de pavages apériodiques sont plus que des curiosités mathématiques. D&rsquo;une part, ils servent de tremplin pour des œuvres d&rsquo;art, comme le carrelage Penrose <a href="https://upload.wikimedia.org/wikipedia/commons/thumb/3/36/Salesforce_Transit_Center_main_entrance.jpg/800px-Salesforce_Transit_Center_main_entrance.jpg?20180817233938" target="_blank" rel="nofollow noopener" data-url="https://upload.wikimedia.org/wikipedia/commons/thumb/3/36/Salesforce_Transit_Center_main_entrance.jpg/800px-Salesforce_Transit_Center_main_entrance.jpg?20180817233938"><u>trouvé au Salesforce Transit Center</u></a><span class="sr-only"> (s&rsquo;ouvre dans un nouvel onglet)</span> à San Francisco, et révèlent que certaines mosaïques islamiques médiévales utilisaient des motifs similaires non répétitifs.</p>
<p>Les pavages apériodiques aident également les physiciens et les chimistes à comprendre la structure et le comportement de <u>quasi-cristaux</u>structures dans lesquelles les atomes sont ordonnés mais n&rsquo;ont pas de motif répétitif.</p>
</div>
<p>[ad_2]</p>
<p><a href="https://www.livescience.com/newly-discovered-einstein-tile-is-a-13-sided-shape-that-solves-a-decades-old-math-problem">Source link </a></p>

La tuile « einstein » récemment découverte est une forme à 13 côtés qui résout un problème mathématique vieux de plusieurs décennies
-
by thebuzzly
#image_title
- Categories: Science
Related Content
Amazon Prime Day est de retour, avec des offres incroyables sur les trackers de fitness
by
thebuzzly
05/07/2023
Économisez 200 $ sur cet élégant rameur Hydrow sur Amazon
by
thebuzzly
05/07/2023
Un singe du zoo mange le cadavre de son bébé après l'avoir transporté pendant des jours
by
thebuzzly
04/07/2023